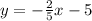Answer:
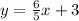 and
and
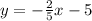
Explanation:
To find the slope (gradient) of a line, choose 2 points on the line and put their coordinates into the formula:
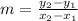
where
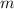 is the slope and
is the slope and
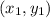 and
and
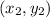 are the 2 points.
are the 2 points.
The y-intercept is the y-coordinate of the point where the line crosses the y-axis.
The question has given you one point that both lines pass through: (-5, -3)
You also need to determine the points where both lines cross the y-axis to determine their y-intercepts - use those as the second points.
From inspection, for the upper line this is (0, 3) and for the other line this is (0, -5)
Therefore, the slope of the upper line is:
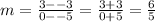
This line crosses the y-axis (0, 3) so its y-intercept is 3
Therefore, the equation is
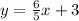
The slope of the lower line is:
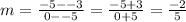
This line crosses the y-axis (0, -5) so its y-intercept is -5
Therefore, the equation is