Question

Last year, Lisa had $30,000 to invest. She invested some of it in an account that paid 10% simple interest per year, and she invested the rest in an account that paid 8% simple interest per year. After one year, she received a total of $2640 in interest. How much did she invest in each account?

Answer 1

In general, the simple interest formula is

`A=P(1+rt)`

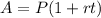
Where t is given in years.

And the interest is given by

`\begin{gathered} I=A-P=P((1+rt)-1)=P(rt) \\ \Rightarrow I=P(rt) \end{gathered}`

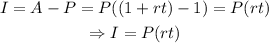
Let B the initial amount Lisa invested in the 10% interest account and C the amount she invested in the 8% account.

Therefore,

`\begin{gathered} B+C=30000 \\ I_B+I_C=2640 \end{gathered}`

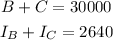
Expanding the second equation,

`\begin{gathered} \Rightarrow B(10\%\cdot1)+C(8\%\cdot1)=2640 \\ \Rightarrow B(0.10)+C(0.08)=2640 \end{gathered}`

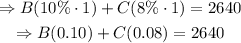
The system of equations becomes

`\begin{gathered} B+C=30000 \\ \text{and} \\ 0.1B+0.08C=2640 \end{gathered}`

From the first equation, B=30000-C. Substitute into the second equation as shown below

`\begin{gathered} B=30000-C \\ \Rightarrow0.1(30000-C)+0.08C=2640 \\ \Rightarrow3000-0.1C+0.08C=2640 \\ \Rightarrow C=(360)/(0.02)=18000 \\ \Rightarrow C=18000 \end{gathered}`

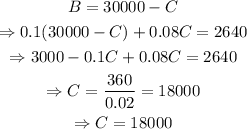
And

`\begin{gathered} C=18000 \\ \Rightarrow B=30000-18000=12000 \\ \Rightarrow B=12000 \end{gathered}`

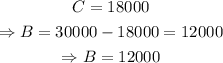
Therefore, she invested $12000 in the 10% account and $18000 in the 8% account.