Given the polynomial function h(x) defined as:

The y-intercept is the value of the function at x = 0. Then, evaluating h(0):
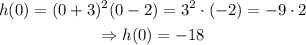
The y-intercept is a unique value, so its multiplicity is 1. On the other hand, the x-intercepts are those x-values such that h(x) = 0. Then, solving the polynomial equation for x:
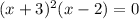
This equation is 0 for:
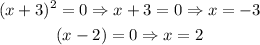
The first equation has a square exponent, so the multiplicity is 2. The multiplicity of the second equation is 1 because it is linear.
Summarizing:
x-intercepts:
i) -3, multiplicity 2
ii) 2, multiplicity 1
y-intercept:
i) -18, multiplicity 1
And the graph of the function looks like this:
For the end behavior, we need to analyze the limits for +∞ and -∞:
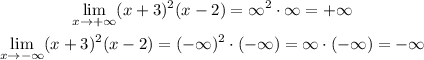
So the function tends to infinite when x tends to infinite, and to minus infinite when x tends to minus infinite.