First of all we are being asked about the probability of a car not needing repairs. We will have to work with the percentages like fractions, for example a 15% chance would be 0.15.
The probability of picking a car that doesn't need repairs ( P(nr) ) can be calculated using the probability of car needing at least one repair ( P(r) ). There are two possible outcomes when you pick a car: or the car needs no repairs or it needs at least one. This means that sum of the probabilities of both outcomes is 1:
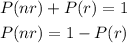
Now, the probability of needing at least 1 repairs P(r) is given by the sum of the probabilities of needing 1, 2, 3 or more repairs. These probabilities are given to us so:
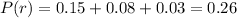
So the probability of needing no repairs is:
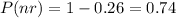
Writting as a percentage the probability of needing no repairs is 74%.
While solving this one we also find the solution for the third item since P(r) is the probability of needing some repairs. Since P(r)=0.26 then that probability is 26%.
For the second item we need to find the probability of needing no more than 1 repair. This probability is given by the probability of needing no repairs and the probability of needing one (and only one) repair. Then:
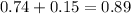
Therefore this probability is 89%.
In summary, the correct answers are 74%, 89% and 26% respectively.