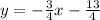To write the equation of a line in the form y=mx+b you need to identify the slope (m) and the y-intercept (b).
Slope:
Two perpendicular lines have opposite reciprocals:
You have the line:
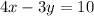
Identify the slope in the equation above (solve the equation for y to get a equation in the form y=mx+b):
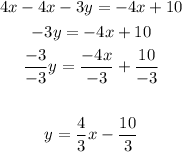
The slope of the perpendicular line (given) is 4/3.
Find the opposite reciprocal to find the slope of the line:
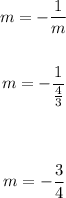
Slope: -3/4
y-intercept:
Use the given point (-7,2) (x= -7 and y= 2) and the slope (m=-3/4) in the equation y=mx+b to solve b:
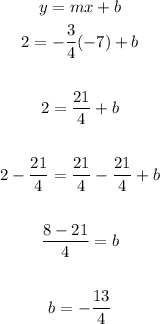
Y-intercept: -13/4Equation of the line: