Question

Mr. Adelson ordered 100 pizzas for a total of $1255. Cheese pizzas cost $11.50 each, and pepperoni pizzas cost $13.00 each. Write a system of equation that can be used to determine, "c," the number of cheese pizzas and "p" the number of pepperoni pizzas that Mr. Adelson should order. Then solve and determine the number of pizza for each. Show your work! 1) Write a system of equations, 2) Solve.

Answer 1

To answer this question, we need to translate the situation into two equations to solve the system of equations.

We have that Mr. Adelson ordered 100 pizzas, and those pizzas are cheese pizzas and pepperoni pizzas. Then, we can say that the sum of both types of pizzas equals 100:

`c+p=100`

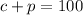
We also have that:

1. Cheese pizzas cost $11.50 each

2. Pepperoni pizzas cost $13.00 each

And Mr. Adelson spent $1255 to buy 100 of both types of pizzas, then, we have:

`11.50\cdot c+13.00\cdot p=1255`

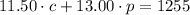
Now, we have the next system, and we could use the substitution method as follows:

Then we can substitute the value of c into the second equation as follows:

`11.50\cdot(100-p)+13.00p=1255`

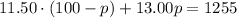
Applying the distributive property:

`1150-11.50p+13.00p=1255`
`1.5p=1255-1150`

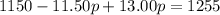
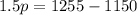
Dividing both sides by 1.5:

`p=(1255-1150)/(1.5)\Rightarrow p=(105)/(1.5)\Rightarrow p=70`

To find the value for the number of cheese pizzas, we can substitute this value of pepperoni pizzas, p = 70, into the first equation:

`c+p=100\Rightarrow c=100-p\Rightarrow c=100-70\Rightarrow c=30`

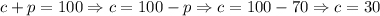
Therefore, we have that Mr. Adelson ordered 30 cheese pizzas and 70 pepperoni pizzas.