Question

2.1.9 An initial investment amount P, an annual interest rate r, and a time t are given. Find the future value of the monthly, (c) daily, and (d) continuously. Then find (e) the doubling time I for the given interest rate. P = $2500, r=3.95%, t = 8 yr a) The future value of the investment when interest is compounded annually is $ 3408.29 (Type an integer or a decimal. Round to the nearest cent as needed.) b) The future value of the investment when interest is compounded monthly is $ (Type an integer or a decimal. Round to the nearest cent as needed.)

Answer 1

When the interest is compounded monthly, we have to do two things:

- Calculate the number of periods: in this case we have 8*12=96 months.

`8\text{years}\cdot12\text{ months/year}=96\text{ months}`

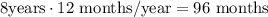
- The monthly interest rate: we have to divide the annual nominal rate by 12 (the number of periods in the year).

`\begin{gathered} r=3.95\text{ \%} \\ r_m=(3.95)/(12)=0.32917\text{ \%} \end{gathered}`

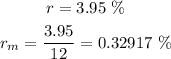
Then, we can calculate the future value as:

`\begin{gathered} FV=C(1+r_m)^m \\ FV=2,500\cdot(1+0.0032917)^(96)=2,500\cdot1.37091864=3,427.30 \end{gathered}`

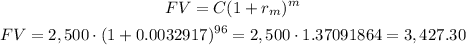
The future value when compounded monthly is $3,427.30.

General formula:

`FV=PV\cdot(1+(r)/(m))^(m\cdot n)`

m: number of subperiods (monthly --> m=12)