Question

An object moving with uniform acceleration has a velocity of 13.0 cm/s in the positive x-direction when its x-coordinate is 3.18 cm. If its x-coordinate 2.95 s later is −5.00 cm, what is its acceleration? cm/s2

Answer 1

Given:

The initial velocity of the object is: u = 13 cm/s

The time taken by an object to change the position coordinate is: t = 2.95 s

The change in the position (displacenent) is: Δx = -5 cm - 3.18 cm = - 1.82 cm

To find:

The acceleration of an object.

Step-by-step explanation:

The acceleration of an object can be determined by using following kinematical equation,

`\Delta x=ut+(1)/(2)at^2`

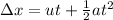
Rearranging the above equation, we get:

`a=(2(\Delta x-ut))/(t^2)`

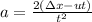
Substituting the values in the above equation, we get:

`\begin{gathered} a=\frac{2*(1.82\text{ cm}-13\text{ m/s}*2.95\text{ s\rparen}}{(2.95\text{ s\rparen}^2} \\ \\ a=\frac{2*(-36.53^\text{ cm})}{8.7025\text{ s}} \\ \\ a=-8.9351\text{ cm/s}^2 \end{gathered}`

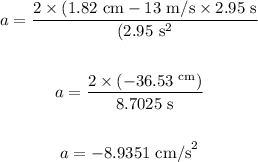
Final answer:

The acceleration of an object is -8.9351 cm/s^2.