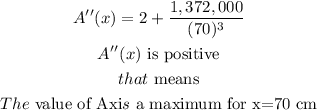Question

box with a square base and open top must have a volume of 171500c * m ^ 3 . We wish to find the imensions of the box that minimize the amount of material used.

Answer 1

step 1

Find out the equation of the volume of the box

`\begin{gathered} V=x^2h \\ V=171,500\text{ cm}^3 \\ 171,500=x^2h \\ h=(171,500)/(x^2) \end{gathered}`

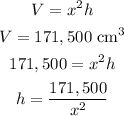
step 2

Find out the expression for the surface area

The surface area is given by the expression

`A=x^2+4xh`

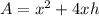
substitute the value of h

`\begin{gathered} A=x^2+4x(171,500)/(x^2) \\ simplify \\ A(x)=x^2+(686,000)/(x) \\ \\ A(x)=(x^3+686,000)/(x) \end{gathered}`

step 3

Find out the derivative A'(x)

`A^(\prime)(x)=2x-(686,000)/(x^2)`

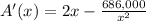
step 4

Equate the derivative to zero

`\begin{gathered} 2x-(686,000)/(x^2)=0 \\ 2x=(686,000)/(x^2) \\ \\ 2x^3=686,000 \\ x^3=343,000 \\ x=70 \end{gathered}`

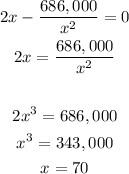
A'(x)=0 when x=70

step 5

Find out the second derivative A''(x)

`A^(\prime)^(\prime)(x)=2+(1,372,000)/(x^3)`

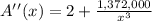
Evaluate the second derivative for x=70

`\begin{gathered} A^(\prime)^(\prime)(x)=2+(1,372,000)/((70)^3) \\ A^(\prime)^(\prime)(x)\text{ is positive} \\ that\text{ means} \\ The\text{ value of A\lparen x\rparen i}s\text{ a maximum for x=70 cm} \end{gathered}`