Question

I need answer on this graphing va substitution.Problem 7 I tried to solve it but not sure that’s correct

Answer 1

Given the system of equations:

`\begin{gathered} 2x+9y=27 \\ x-3y=-24 \end{gathered}`

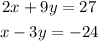
To solve it by substitution, follow the steps below.

Step 1: Solve one linear equation for x in terms of y.

Let's choose the second equation. To solve it for x, add 3y to each side of the equations.

`\begin{gathered} x-3y=-24 \\ x-3y+3y=-24+3y \\ x=-24+3y \end{gathered}`

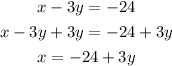
Step 2: Substitute the expression found for x in the first equation.

`\begin{gathered} 2x+9y=27 \\ 2\cdot(-24+3y)+9y=27 \\ -48+6y+9y=27 \\ -48+15y=27 \end{gathered}`

Step 3: Isolate y in the equation found in step 2.

To do it, first, add 48 to both sides.

`\begin{gathered} -48+15y=27 \\ -48+15y+48=27+48 \\ 15y=75 \end{gathered}`

Then, divide both sides by 15.

`\begin{gathered} (15y)/(15)=(75)/(15) \\ y=5 \end{gathered}`

Step 4: Substitute y by 5 in the relation found in step 1 to find x.

`\begin{gathered} x=-24+3y \\ x=-24+3\cdot5 \\ x=-24+15 \\ x=-9 \end{gathered}`

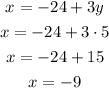
Answer:

x = -9

y = 5

or (-9, 5)

Also, you can graph the lines by choosing two points from each equation, according to the picture below.