Question

2 Here are two equations:Equation 1: 6x + 4y = 34Equation 2: 5x – 2y = 15ide whether each (x, y) pair is a solution to one equation, both equations, ora. Decide whether eacneither of the equations,i (3,4)ii. (4,2.5)ill. (5,5)iv. (3,2)b. Is it possible to have more than one (x, y) pair that is a solution to bothequations? Explain or show your reasoning,what is the Explanation to show my reasoning

Answer 1

To check if the pairs are solution to the system of equations we need to replace the values of "x" and "y" on each equation of the system and check if they're valid for hat pair. We have:

a) (3, 4).

First equation:

`\begin{gathered} 6x+4y=34 \\ 6\cdot3+4\cdot4=34 \\ 18+16=34 \\ 34=34 \end{gathered}`

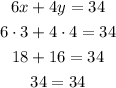
The equation is valid, so the pair is a solution to the first equation.

Second equation:

`\begin{gathered} 5x-2y=15 \\ 5\cdot3-2\cdot4=15 \\ 15-8=15 \\ 7=15 \end{gathered}`

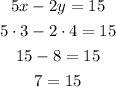
The equation is invalid, so the pair is not a solution to the second equation.

b) (4, 2.5)

First equation:

`\begin{gathered} 6\cdot(4)+4\cdot(2.5)=34 \\ 24+10=34 \\ 34=34 \end{gathered}`

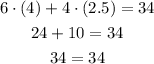
The equation is valid, so the pair is a solution to the first equation.

Second equation:

`\begin{gathered} 5\cdot4-2\cdot2.5=15 \\ 20-5=15 \\ 15=15 \end{gathered}`

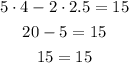
The equation is valid, so the pair is a solution to the second equation.

The pair is a solution to both equations.

c) (5,5)

First equation:

`\begin{gathered} 6\cdot5+4\cdot5=34 \\ 30+20=34 \\ 50=34 \end{gathered}`

The equation is invalid, so the pair is not a solution to the first equation.

Second equation:

`\begin{gathered} 5\cdot5-2\cdot5=15 \\ 25-10=15 \\ 15=15 \end{gathered}`

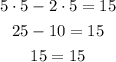
The equation is valid, so the pair is a solution to the second equation.

d) (3,2)

First equation:

`\begin{gathered} 6\cdot3+4\cdot2=34 \\ 18+8=34 \\ 26=34 \end{gathered}`

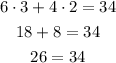
The equation is invalid, so the pair is not a solution to the first equation.

Second equation:

`\begin{gathered} 5\cdot3-2\cdot2=15 \\ 15-4=15 \\ 11=15 \end{gathered}`

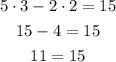
The equation is invalid, so the pair is not a solution to the second equation.

b) Is it possible to have more than one pair that is a solution to both equations?

To check the number of equations a system has we can divide the numbers that multiply x and y on each equation.

`\begin{gathered} (x_1)/(x_2)=(6)/(5) \\ \\ (y_1)/(y_2)=(4)/(-2)=-2 \end{gathered}`

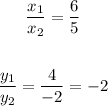
When they are different the system only has one solution. This happens because the slope of each equation is different, therefore they only intersect once. In order for a system to have more than one solution the equations must have the same slope and pass through the same points.