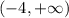Given the statement:
"Six more than b exceeds 2"
-The first part, six more than b can be expressed as a sum, you have to add 6 to the variable "b".
-The word "exceeds" indicates that the previous part of the sentence is greater than the second part, to express this you have to use the symbol ">"
The inequality can be written as:

The next step is to solve the inequality for b, to do so you have to pass "6" to the right side of the inequality by applying the opposite operation to both sides of it:
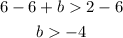
This expression indicates that the variable "b" can take values greater than -4. Note that the symbol ">" does not include the equal sign, which means that "-4" is not included in the interval of definition for the possible values of "b".
To draw this in the number line, you have to start from -4 and draw the line towards +∞, and, since the initial value is not included, you have to draw a blank dot at the endpoint of the line:
To express the inequality as an interval you have to use round brackets, this way you will indicate that the values at the endpoints are not included: