Question

Find the number of permutations of letters in the wordEFFECTIVE

Answer 1

To determine the distinguishable permutations of the given word, here are the steps.

1. Count the number of letters in the given word. In the word EFFECTIVE, there are 9 letters.

2. Calculate 9!.

`9!=9*8*7*6*5*4*3*2*1=362,880`

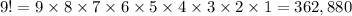
3. Determine what are the letters found in the word effective and count how many times the letter occurred.

Letter E - 3 times

Letter F - 2 times

Letter C - 1 time

Letter T - 1 time

Letter I - 1 time

Letter V - 1 time

4. Get the product of the factorial of the letters that occurred more than once.

`3!*2!=(3*2*1)*(2*1)=12`

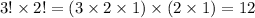
5. Divide the result of step 2 by the result of step 4.

`362,880/12=30,240`

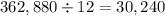
Therefore, there are 30,240 different permutations of the word EFFECTIVE.