Notice that between the tree (represented by a vertical segment), the ground (represented by a horizontal segment), and the rays of the sun (that go from the top of the tree to the ground), we are in the presence of a right angle triangle that has a short leg of size 15 yards (verticel segment), and a long leg of size 17 yards.
Then the angle of elevation is assicuated with the tangent function in that right angle triangle:
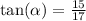
This is the quotient of the side opposite to the angle divided the side adjacent to the angle. Then we can solve for the angle by using the arctangent the following way:
arctan(15/17) (this is what you type in your calculator, but make sure your answer comes in DEGREES. (you need to set your calculator for that)
As I do it in my calculator, I get that the angle is: 41.42366 degrees
And since they want us to round it to the nearest tenth, we give:
angle of elevation = 41.4 degrees.