Question

Graph the following function by considering how the function x^2 has been shifted, reflected, stretched or compressed.

Answer 1

Given the quadratic function g(x) defined as:

`g(x)=-((x-2)^2)/(2)-2`

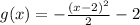
We can go from the function f(x) = x² to g(x) making the transformations:

1) A reflection about the x-axis:

`f(x)\to-f(x)`

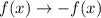
2) A horizontal dilation by a factor of 1/2:

`f(x)\to(1)/(2)f(x)`

3) A shift of 2 units down:

`f(x)\to f(x)-2`

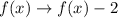
4) A shift of 2 units right:

`f(x)\to f(x-2)`

Combining all these transformations:

`f(x)\to-(f(x-2))/(2)-2=-((x-2)^2)/(2)-2=g(x)`

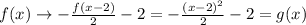
Then, the graphs of f(x) (red) and g(x) (green) are: