Question

z varies directly with x and inversely with y.When x = 6 and y = 2, z = 15What is the value of z when x = 4 and y = 9?

Answer 1

It is given that z varies directly with x and inversely with y.

`z=(kx)/(y)`

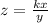
Where k is the constant of proportionality.

First, let us find the value of constant (k).

Substitute x = 6, y = 2, and z = 15

`\begin{gathered} 15=(k\cdot6)/(2) \\ k\cdot6=2\cdot15 \\ k\cdot6=30 \\ k=(30)/(6) \\ k=5 \end{gathered}`

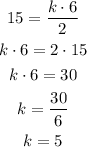
So, the value of k is 5

`z=(5\cdot x)/(y)`

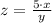
Finally, let us find the value of z when x = 4 and y = 9

`\begin{gathered} z=(5\cdot4)/(9) \\ z=(20)/(9) \end{gathered}`

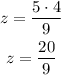
Therefore, the value of z is 20/9