Given:
The radius of the curvature of the convex mirror is

The distance of the object is

Required: image distance and the magnification
Explanation:
first, we find the focal length of the mirror by the relation is
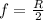
plugging the values in the above, we get
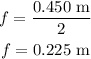
the mirror formula is given by
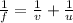
Plugging all the values in the above relation, we get
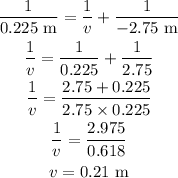
the distance of the image is 0.21 m. it will be formed behind the mirror.
now calculate the magnification. magnification is given by
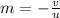
Plugging all the values in the above, we get
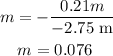
The magnification is 0.076.
the image formed by the convex mirror is virtual, inverted, and erect.