To answer the questions of the problem we have to write the ellipse in standard form, to do this we have to complete squares in each variable. Let's do this:

Now that we have the ellipse written in this form we can start to answer the questions.
1. The ellipse is an horizontal ellipse. This follows from the fact that the denominator in the x variable is greater than the one in the y variable.
To find the vertex and the focus we first need to find some other information of the ellipse. We have to compare our ellipse with the formula:
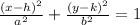
Then we conclude that the cencter of our ellipse is the point (2,-4) and that
a=6 and b=2.
We know that the vertex are a distance a of the center of the ellipse. Since this a horizontal ellipse we have to add ans substract the length a to the x component of the center. With that in mind
2. The coordinates of the left vertex are (-4,-4)
3. The coordinates of the right vertex are (8,-4)
To find the focus we need to find the length c defined as:
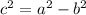
Then,
![\begin{gathered} c^2=36-4 \\ c^2=32 \\ c=\sqrt[]{32} \\ c=5.66 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/yjojsa7ird8rds9sgaz0.png)
With this length we can find the focus, the same way we found the vertex but using the length c instead of a.
4. The left focus has coordinates (-3.66,-4)
5. The right focus has coordinates (7.66,-4)
6. Finally the eccentricity is

All of this can be seen in the graph of the ellipse: