Given the Polynomial Function in the form:
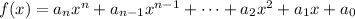
1. This is the Leading Coefficient:
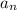
And this is the Constant term:
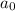
The Rational Root Theorem states that a Rational Root of the function has this form:

Where "p" is a factor of the Constant Term, and "q" is a factor of the Leading Coefficient.
In this case, you know that this is a root of the function f(x):
That indicates that when you substitute that root into the function, you will obtain that:
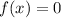
Because, by definition, the roots of a function are the x-intercept, and the y-value is zero when the function intersects the x-axis.
Then, in order to solve the exercise, you must substitute the root into the function and make the function equal to zero:

2. The exercise indicates that you must;
(a) Subtract the Constant Term from both sides of the equation:

(b) Now you have to multiply both sides of the equation by:
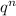
But first you can rewrite the equation applying the Power of Quotients Property, which states that:
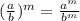
Then:

Therefore, multiplying both sides by the term shown before:
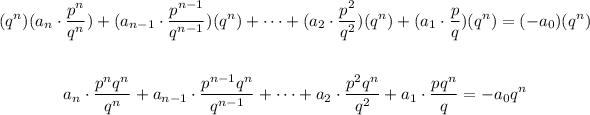
Now that you set up the multiplication you need to apply the Quotient of Powers Property to simplify the terms on the left side. This states that:

Therefore, since in the numerator and in the denominator you have the same base "q", you can subtract the exponents:

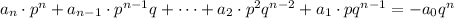
(c) The Greatest Common Factor (GCF) is the largest factor all the terms have in common. In this case, there every term in the equation has a factor "p". Therefore:

Then, you can factor it out:

Remember that according to the Product of Powers Property, when two powers with equal bases are multiplying, you have to add the exponents. You need to keep in mind this property to factor it out.
(d) Knowing that both sides of the equation must be integers and knowing that "p" and "q" have no factors in common, you can conclude that "p" can only divide the Constant Term. Then:

That means that "p" is a factor of the Constant Term.
Hence, the answers are:
1.

2. (a)

(b)
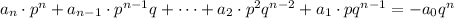
(c)

(d) It means that "p" is a factor of the Constant Term.