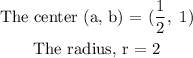Question

I have a class to finish it ends in two days

Answer 1

Answer:
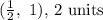
`((1)/(2),\text{ 1), 2 units}`Explanations:

The given equation is:

`x^2+y^2-x-2y-(11)/(4)=\text{ 0}`

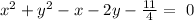
The standard equation of a circle is given as:

(x - a)² + (y - b)² = r²

where (a, b) is the center

r is the radius

Express the given equation in form of the standard equation

Collect like terms

`x^2-x+y^2-2y\text{ = }(11)/(4)`

Add the squares of the half of the coefficients of x and y to both sides of the equation

`\begin{gathered} x^2-x+((-1)/(2))^2+y^2-2y+(-1)^2=(11)/(4)+((-1)/(2))^2+(-1)^2_{} \\ x^2-x+((1)/(2))^2+y^2-2y+1^2=(11+1+4)/(4) \\ (x-(1)/(2))^2+(y-1)^2=(16)/(4) \\ (x-(1)/(2))^2+(y-1)^2=\text{ 4} \\ (x-(1)/(2))^2+(y-1)^2=2^2 \end{gathered}`

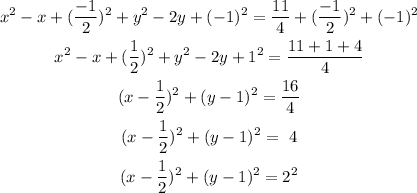
Compare the resulting equation with (x - a)² + (y - b)² = r²

`\begin{gathered} \text{The center (a, b) = (}(1)/(2),\text{ 1)} \\ \text{The radius, r = 2} \end{gathered}`