Question

a) Find the probability that the match ends in a draw.b) Calculate the expected point that the team will get in the match.

Answer 1

Part A. To determine the probability that the match ends in a draw we need to use the fact that the sum of the probabilities of all possible outcomes must add up to 1. Therefore, since the possible outcome is that the team wins the match, loses the match or ends in a draw we have that:

`P(win)+P(lose)+P(draw)=1`

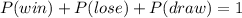
Now, we subtract the probability of winning and losing:

`P(draw)=1-P(win)-P(lose)`

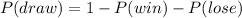
Substituting the values we get:

`P(draw)=1-0.5-0.3`

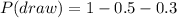
Solving the operations:

`P(draw)=0.2`

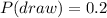
Therefore, the probability of a draw is 0.2.

Part B. The expected value is the product of the number of points for each outcome and the corresponding probability. Therefore, the expected value of points is:

`E(x)=(2)P(win)+(0)P(lose)+(1)P(draw)`

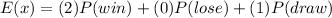
now, we substitute the probabilities:

`E(x)=(2)(0.5)+(0)(0.3)+(1)(0.2)`

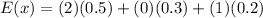
Solving the operations:

`E(x)=1.2`

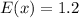
Therefore, the expected number of points is 1.2