13 minutes
Step-by-step explanationStep 1
find the distance to thunder
a) let d represents the distance
let t represents the time,
the distance traveled by the ligth is given by:
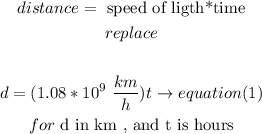
and
the distance traveled by the sound
i) convert the 9.8 seconds into hours
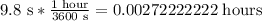
and

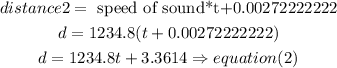
use equation (1) and equatin (2) to solve for t

now, replace in the equation (1) to find the distance
![\begin{gathered} d=(1.08*10^9(km)/(h))t\operatorname{\rightarrow}equat\imaginaryI on(1) \\ d=(1.08*10^9(km)/(h))3.11*10^(-9)\text{ hours\rparen} \\ d=3.36\text{ km} \end{gathered}]()
so,
the distance to the center of the sterom is 3.36 Km
Step 2
now, to know the time of the storm to arrive, we need to aply the formula

finally, to conver from hours to miinutes, multiply by 60
so
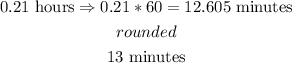
therefore, the answer is 13 minutes
I hope this helps you