Question

Suppose that you drive 30000 miles per year and gas averages $4 per gallon complete part A and B

Answer 1

Problem says you drive 30,000 miles per year and gas averages $4 per gallon.

a. If you own a hybrid car averaging 30 miles per gallon, then annually you will consume the next amount of gallons:

`30,000\text{miles x}(1gallon)/(30miles)=1,000gallons`

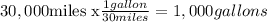
And you will pay for 1000 gallons:

`1000\text{gallons}(4dollars)/(1gallon)=4000\text{ dollars}`

But, if you own a SUV averaging 9 miles per gallon, you'll consume the next amount of gallons:

`30,000\text{miles x}(1gallon)/(9miles)=3,333.3gallons`

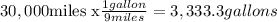
And you will spend in fuel:

`3333.3\text{gallons}(4dollars)/(1gallon)=13333.3\text{ dollars}`

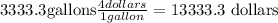
Thus, if you own a hybrid car, you will save in annual fuel expenses:

`13333.3-4000=9333.3\approx9333dollars`

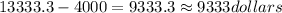
b. If you deposit your monthly fuel savings at the end of each month into an annuity that pays 4.8% compounded monthly, at the end of four years you will save:

The formula is:

`A=(P\lbrack(1+(r)/(n))^(nt)-1\rbrack)/(((r)/(n)))`

Where A is the balance in the account after t years, P is the amount you deposit each month, r is the annual interest rate in decimal form and n is the number of compounding periods in one year (12 as it is monthly).

Then, if you save annually $9333, each month you save $9333/12=$777.75

At the end of 4 years, you will save then:

`\begin{gathered} A=(777.75\lbrack(1+(0.048)/(12))^(12\cdot4)-1\rbrack)/(((0.048)/(12))) \\ A=(777.75\lbrack(1+0.004)^(48)-1\rbrack)/((0.004)) \\ A=(777.75\lbrack(1.004)^(48)-1\rbrack)/((0.004)) \\ A=(777.75\lbrack1.2112-1\rbrack)/((0.004)) \\ A=(777.75*0.2112)/((0.004)) \\ A=41066.5\approx41067 \end{gathered}`

After 4 years you will save $41067