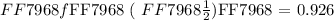Question

Y = (x)^(1/9)*Find f(x) when x=(1/2)Round your answer to the nearest thousandth.

Answer 1

We are given a function f ( x ) defined as follows:

`y=f(x)=x^{(1)/(9)}`

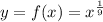
We are to determine the value of f ( x ) when,

`*\text{ = }(1)/(2)`

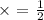
In such cases, we plug in/substitue the given value of x into the expressed function f ( x ) as follows:

`y\text{ = f ( }(1)/(2)\text{ ) = (}(1)/(2))^{(1)/(9)}`

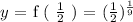
We will apply the power on both numerator and denominator as follows:

`f((1)/(2))=\frac{1^{(1)/(9)}}{2^{(1)/(9)}}\text{ = }\frac{1}{2^{(1)/(9)}}`

Now we evaluate ( 2 ) raised to the power of ( 1 / 9 ).

`f\text{ ( }(1)/(2)\text{ ) = }(1)/(1.08005)`

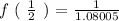
Next apply the division operation as follows:

`f\text{ ( }(1)/(2))\text{ = }0.92587`

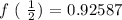
Once, we have evaluated the answer in decimal form ( 5 decimal places ). We will round off the answer to nearest thousandths.

Rounding off to nearest thousandth means we consider the thousandth decimal place ( 3rd ). Then we have the choice of either truncating the decimal places ( 4th and onwards ). The truncation only occurs when (4th decimal place) is < 5.

However, since the (4th decimal place) = 8 > 5. Then we add ( 1 ) to the 3rd decimal place and truncate the rest of the decimal places i.e ( 4th and onwards ).

The answer to f ( 1 / 2 ) to the nearest thousandth would be:

`\textcolor{#FF7968}{f}\text{\textcolor{#FF7968}{ ( }}\textcolor{#FF7968}{(1)/(2))}\text{\textcolor{#FF7968}{ = 0.926}}`