Answer
Question 4
Option A is correct.
9⁻⁵
Question 5
Option C is correct.
2⁷
Question 6
Option B is correct.
Yes, both expressions are equal to 10⁻⁶
Question 7
3⁰ + 3⁻² = 1 (1/9) = (10/9)
Step-by-step explanation
To answer these questions, we will use the laws of indices.
- When a variable carries a power and is raised to an extra power, the answer is the variable carrying the product of these two powers.
- When a variable is raised to the power of a negative number, this is the same as 1 over that variable raised to the positive value of that power
- When the same variable, carrying different powers are multiplied with each other, then, the result is that same variable raised to the power of the sum of the two powers from before multiplication.
- When any number or variable is raised to the power of 0, the answer is 1.
Question 4
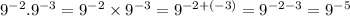
Question 5
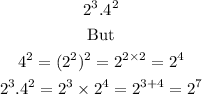
Question 6
To know the answer to this, we will solve the two expressions
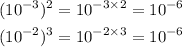
We can see that both expressions are equal to 10⁻⁶
Question 7
3⁰ + 3⁻²
3⁰ = 1
3⁻² = (1/3²) = (1/9)
3⁰ + 3⁻² = 1 + (1/9) = 1 (1/9) = (10/9)
Hope this Helps!!!