Answer:
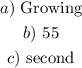
Step-by-step explanation:
Here, we want to define the terms in the given exponential equation
The general form is:
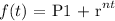
P represents the initial value, while r represents the percentage change and t represents the time frame
if the value inside the bracket is greater than 1, we have an increase
We could rewrite the equation as:
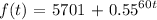
This means that:
The function is growing exponentially at a rate of 55% every second