Question

Find the length of the diagonal of a square with perimeter 32.A.
`4 √(2)`B. 8C.
`2 √(2)`D. 45E.
`8 √(2)`

Answer 1

`E.8\sqrt[]{2}`

Step-by-step explanation

The square has a perimeter of 32.

The perimeter of a square is given as:

`P=4\cdot L`

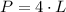
where L = length of the side of the square

Therefore, we have that for the given square:

`\begin{gathered} 32=4\cdot L \\ \Rightarrow L=(32)/(4) \\ L=8 \end{gathered}`

The square has sides 8 units long.

To find the length of the diagonal, apply Pythagoras theorem, since the diagonal forms a right triangle with the sides of the square:

`\text{hyp}^2=a^2+b^2`

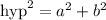
where hyp = hypotenuse of the triangle (diagonal)

a, b = legs of the triangle (side lengths of the square)

Therefore, we have that:

`\begin{gathered} D^2=8^2+8^2 \\ D^2=64+64=128 \\ D=\sqrt[]{128} \\ D=8\sqrt[]{2} \end{gathered}`

That is the length of the diagonal.