Question

Provide the required features of each vertex form quadratic function then convert it into standard form. 1. f(x) = (x - 4)' + 9Axis of Symmetry: Vertex: Maximum or Minimum: Domain: Range:y-intercept:roots: 2- f(x) =- 2(x + 2)² – 1 Axis of Symmetry: Vertex: Maximum or Minimum: Domain: Range:y-intercept:roots: Show work

Answer 1

Given

`f(x)=(x-4)^2+9`

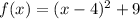
Procedure

Let's start by graphing the function

Now we are going to calculate each of the items

Axis of symmetry (x = 4)

The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves.

quadratic function in standard form

y = ax^2 + bx + c

`\begin{gathered} y=x^2-8x+16+9 \\ y=x^2-8x+25 \end{gathered}`
`x=-(b)/(2a)=-(-8)/(2\cdot1)=4`

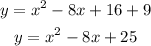
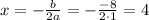
Vertex (4, 9)

The vertex of a parabola is the highest or lowest point, also known as the maximum or minimum of a parabola.

Vertex form

`y=a(x-h)^2+k`

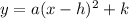
x = 4, y = 9

Maximum or minimum (minimum)

Whether the parabola is a max or a min depends on the value of a

a>0 minimum

a<0 maximum

Domain (All real numbers)

The domain of a function is the complete set of possible values of the independent variable.

The domain would be all real values

Range (y >= 9)

The set of all output values of a function.

We can see in the graph that the values are greater than 9

y-intercept (0, 25)

Where a line crosses the y-axis of a graph. Just find the value of y when x equals 0.

`\begin{gathered} f(0)=(0+4)^2+9 \\ f(0)=16+9 \\ f(0)=25 \end{gathered}`

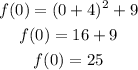
Roots (no roots)

Roots are also called x-intercepts or zeros.

We can see that there are no intersections with the x-axis in the figure.