Question

An economist wants to estimate the mean per capita income in thousands of dollars for a major city in California. He believes that the mean income is $24.4 and the standard deviation is known to be $8.1. How large of a sample would be required in order to estimate the mean per capita income at the 80% level of confidence with an error of at most $0.24 round your answer to the next integer

Answer 1

Step-by-step explanation:

The formula for calculating the MSE and then the confidence interval is as follows:

`MSE\text{ = z * }(\sigma)/(√(n))`

We are given that the standard deviation is $8.1 and that MSE = $0.24.

We are also told that the confidence level is 80%. The corresponding z value at 80% is 1.28

We are then required to calculate n:

`\begin{gathered} 0.24\text{ = 1.28 * }(8.1)/(√(n)) \\ (16)/(3)\text{ = }(√(n))/(8.1) \\ 43.2\text{ = }√(n) \\ 1866.24\text{ = n} \\ n\text{ }\approx\text{ 1866} \end{gathered}`

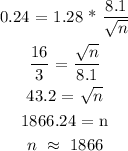
Answer: n = 1866