Question

Environmental Science The spread of a contaminant is increasing in a circularpattern on the surface of a lake. The radius of the contaminant can be modeledby r(t) = 5.25Vr, where r is the radius in meters and + time in hours since contamination. Recall,the formula for the area of circle, A(r) = Tr?a) Using the terms: function, inputs, and outputs, explain the meaning of the mathematicalexpression, (A or) (36).b)in the context of the situation, interpret The meaning of a function (A o r)(t).c) Use A(+(1) = 7(5.25VT) to find the size of the contaminated area after 36 hours.d)Find when the size of the contaminated area is 6250 square meters.

Answer 1

(a)

The function

`(A\circ r)(36)`

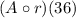
means that the input of the function is 36 and the output is the value that we get when we input 36 onto the function r which is put on the function A.

(c)

Let's find the composite function

`(A\circ r)=\pi(5.25\sqrt[]{t})^2`

Now, we find the value of (A o r) (36):

`\begin{gathered} (A\circ r)(36)=\pi(5.25\sqrt[]{36})^2 \\ =\pi(5.25(6))^2 \\ =3117.25 \end{gathered}`

So the size of contamination is approximately 3117.25 sq. m.

(d)

We want the time (t) when the size of the contamination would be 6250. Let's find it:

`\begin{gathered} (A\circ r)=\pi(5.25\sqrt[]{t})^2 \\ 6250=\pi(5.25\sqrt[]{t})^2 \\ (6250)/(\pi)=(5.25\sqrt[]{t})^2 \\ 5.25\sqrt[]{t}=\sqrt[]{(6250)/(\pi)} \\ \sqrt[]{t}=\frac{\sqrt[]{(6250)/(\pi)}}{5.25} \\ t=(\frac{\sqrt[]{(6250)/(\pi)}}{5.25})^2 \\ t=(\frac{\frac{\sqrt[]{6250}}{\sqrt[]{\pi}}}{5.25})^2 \\ t=\frac{(\frac{\sqrt[]{6250}}{\sqrt[]{\pi}})^2}{(5.25)^2} \\ t=((6250)/(\pi))/(27.5625) \\ t\approx72.18 \end{gathered}`Answer - About 72.18 hours