Let's find the measure of the missing angles.
• Measure of angle h:
Apply the vertical angles theorem.
Vertically opposite angles are congruent.
m∠h = 60 degrees
• Measure of angle g:
We know that angles 60 + f + g + h = 360 (a circle)
m∠f = m∠g
Thus, we have:
m∠g + m∠g = 360 - 60 - 60
2m∠g = 240
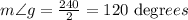
m∠g = 120 degrees
• Measure of angle f:
m∠f = m∠g
Thus, we have:
m∠f = 120 degrees
• Measure of angle k:
Apply the linear pair of angles theorem,
If 2 angles form a linear pair, they are supplementary. Suplementary angles sum up to 180 degrees.
Thus,
m∠k + 124 = 180
Subtract 124 from both sides:
m∠k + 124 - 124 = 180 - 124
m∠k = 56 degrees
• Measure of angle j:
Apply the vertical angles theorem.
Vertical angles are congruent.
Therefore,
m∠j = 124 degrees
• Measure ,of angle i:
Apply the vertical angles theorem.
m∠i = m∠k
m∠i = 56 degrees
• Measure of angle d:
Angle d is a right angle.
Thus, we have:
m∠d = 90 degrees
• Measure of angle b:
m∠b = 90 degrees
• Measure ,of angle c:
m∠c + 64 = 90
Subtract 64 from both sides:
m∠c + 64 - 64 = 90 - 64
m∠c = 26 degrees
• Measure of angle e:
m∠e = m∠c
m∠e = 26 degrees
• Measure of angle a
m∠a = 64 degrees
ANSWER:
m∠a = 64 degrees
m∠b = 90 degrees
m∠c = 26 degrees
m∠d = 90 degrees
m∠e = 26 degrees
m∠f = 120 degrees
m∠g = 120 degrees
m∠h = 60 degrees
m∠i = 56 degrees
m∠j = 124 degrees