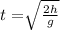Question

Using function notation, how would we represent when an object hitsthe ground if time is measured in seconds and height is measured infeet?

Answer 1

The height h(t) of a projectile above the ground after t seconds is given by; (neglecting air resistance)

`h(t)\text{ = -(}(1)/(2))gt^2+v_{0_{}}t+h_0`

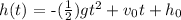
where;

`\begin{gathered} v_0\text{ = initial velocity} \\ h_0=\text{ initial height} \\ h\mleft(t\mright)=height\text{ at time t} \\ g\text{ = acceleration due to gravity} \\ t\text{ = time in seconds} \end{gathered}`

when the object hits the ground, the height h(t) will be equal to zero.

`h(t)\text{ = 0}`

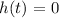
so, from the height equation at time t when the height h(t) is zero, the equation becomes;

`\begin{gathered} h(t)\text{ = -(}(1)/(2))gt^2+v_{0_{}}t+h_0\text{ = }0 \\ \text{-(}(1)/(2))gt^2+v_{0_{}}t+h_0\text{ = }0\text{ }\ldots\ldots\ldots\ldots1 \end{gathered}`

The time when the object hits the ground can be represented by the equation 1 above.

By substituting the values of g,v and h respectively we can solve for t.

Assumming the object was dropped on a free fall from height h.

For free fall the initial velocity is zero.

`\begin{gathered} v_{0\text{ }}=0 \\ h_0\text{ = h} \end{gathered}`

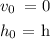
Substituting this values into the equation 1 above, we have:

`\begin{gathered} \text{-(}(1)/(2))gt^2+(0)_{}t+\text{ h }=\text{ 0} \\ \text{-(}(1)/(2))gt^2+\text{ h }=\text{ 0} \end{gathered}`

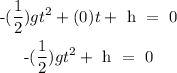
Then solving for t, we have;

`\begin{gathered} \text{-(}(1)/(2))gt^2+\text{ h }=\text{ 0} \\ \text{-(}(1)/(2))gt^2=\text{ -h} \\ \text{divide through by }-((1)/(2))g \\ t^2\text{ }=\text{ }(-h)/(-((1)/(2))g) \\ t^2\text{ }=(2h)/(g) \\ \text{square root both sides;} \\ t\text{ =}\sqrt{(2h)/(g)} \end{gathered}`

Therefore, In function notation, the time t in seconds when an object dropped from height h(in feet) hits the ground is:

`t\text{ =}\sqrt{(2h)/(g)}`