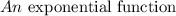Given:
Required:
We need to find the first differences, second differences, and first difference ratios.
Step-by-step explanation:
Recall that the first difference is the difference between values of the dependent variable by subtracting the previous value from each.
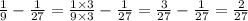
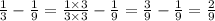
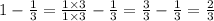
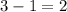
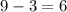
Recall that the second difference is the difference of the first difference.
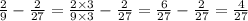


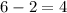
Divide the second number by the first number to find the ratio of the two numbers in the first difference.
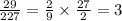

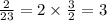
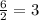
We get the ratio of the first difference is constant so the given function is an exponential function.
Final answer: