Question

You and your sister have been saving and decide to buy a Playstation 5 together. You need $500 to buy the Playstation. Together you have $850 saved up. Since you have more money, you contribute 50% of your savings and your sister contributes 75% of hers toward the $500 cost. How much do each of you have saved individually?Write a system of equations in standard form to model this situation Solve this system of equation using elimination Why might elimination be a good solution method to use in this instance?

Answer 1

- Let the amount you have saved up be x and the amount your sister has saved up be y.

- We are told that together, you both have $850 saved up. This implies that

`x+y=850\text{ \lparen Equation 1\rparen}`

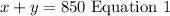
- We are also told that you contribute 50% of your savings. That is,

`50\%\text{ of }x=(50)/(100)* x=0.5x`

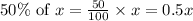
- We are also told that your sister contributes 75% of hers. That is,

`75\%\text{ of }y=(75)/(100)* y=0.75y`

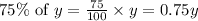
- Since your contributions is towards buying the $500 Playstation, we can say:

`0.5x+0.75y=500\text{ \lparen Equation 2\rparen}`

Question 1:

- Thus, the system of equations is

`\begin{gathered} x+y=850\text{ \lparen Equation 1\rparen} \\ 0.5x+0.75y=500\text{ \lparen Equation 2\rparen} \end{gathered}`

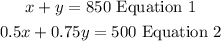
Question 2:

- To solve the question using elimination, we need to make the coefficients of either x or y the same for both equations. We can simply do this by multiplying Equation 1 by 0.75 or 0.5 to make the coefficients of y or x respectively, be the same in both equations

`\begin{gathered} \text{ Multiply Equation 1 by 0.5} \\ 0.5(x+y)=0.5*850 \\ 0.5x+0.5y=425\text{ \lparen Equation 3\rparen} \\ 0.5x+0.75y=500\text{ \lparen Equation 2\rparen} \\ \\ \text{ Subtract Equation 3 from Equation 2, we have:} \\ 0.5x+0.75y-(0.5x+0.5y)=500-425 \\ 0.5x+0.75y-0.5x-0.5y=75 \\ 0.25y=75 \\ \text{ Divide both sides by 0.25} \\ y=(75)/(0.25) \\ \\ \therefore y=300 \\ \\ \text{ Substitute the value of y into any of the 3 equations} \\ \text{ In Equation 1:} \\ x+y=850 \\ x+300=850 \\ \text{ Subtract 300 from both sides} \\ x=850-300 \\ x=550 \end{gathered}`

- The solution to the system of equations is: x = 550, y = 300

Question 3:

- Elimination is a good way to solve the question because the coefficients of Equation 1 are both 1. Thus, we can easily create a new Equation that can have its x or y-term eliminated when added or subtracted to or from another equation.