Question

The lifespan of pet goldfish is a normally distributed random variable. The mean lifespan is 210 days with a standard deviation of 22 days.In a random sample of 50 pet goldfish, how many would you expect to live between 166 and 254 days?Your answer should include both a numerical component and a justification component.

Answer 1

Z-score is computed as follows:

`z=(x-\mu)/(\sigma)_{}`

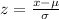
where,

x: observed value

μ: mean

σ: standard deviation

Substituting with x = 166, μ = 210, and σ = 22, we get:

`\begin{gathered} z_1=(166-210)/(22)_{} \\ z_1=-2 \end{gathered}`

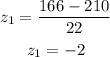
Substituting with x = 254, μ = 210, and σ = 22, we get:

`\begin{gathered} z_2=(254-210)/(22)_{} \\ z_2=2 \end{gathered}`

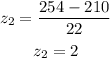
Now, we need to find P(-2From the above graph, P(-2This means that 95.44% of the sample is between the z-scores -2 and 2.

In the context of this problem, 50x95.44% = 47.72 ≈ 47 goldfish are expected to live between 166 and 254 days.