Question

Two strings are made of the same material. String 1 has radius r1 while string 2 has radius r2 = r1/2. When stretched by the same tension, the respective speed of propagation of waves v1 and v2 satisfy the conditionSelect one:a. v1 = 2v2b. None of the above.c. v1 = v2/4d. v1 = v2/2

Answer 1

Given data:

The radius of the first string is r_1.

The radius of the second string is r_2.

The relation between the radius of both the strings is,

`r_2=(r_1)/(2)`

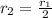
The speed of the propagation of the first wave is v_1.

The speed of propagation of the second wave is v_2.

Solution:

The speed of the propagation in terms of the radius of first string is,

`v_1=(1)/(r_1)\sqrt[]{(T)/(\pi\rho)}`

where,

`\rho\text{ is the density of the string}`

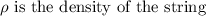
As, both the strings are made of the same material, thus, the density of both the strings remains the same.

The tension along both the strings is the same.

Thus, the speed of propagation of the second string is,

`v_2=(1)/(r_2)\sqrt[]{(T)/(\pi\rho)}`

By dividing both the equations,

`\begin{gathered} (v_1)/(v_2)=\frac{(1)/(r_1)\sqrt[]{(T)/(\pi\rho)}}{(1)/(r_2)\sqrt[]{(T)/(\pi\rho)}} \\ (v_1)/(v_2)=((1)/(r_1))/((1)/(r_2)) \\ (v_1)/(v_2)=(r_2)/(r_1) \end{gathered}`

Substituting the known values,

`\begin{gathered} (v_1)/(v_2)=((r_1)/(2))/(r_1) \\ (v_1)/(v_2)=(1)/(2) \\ v_1=(v_2)/(2) \end{gathered}`

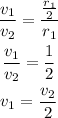
Thus, option d is the correct answer.