Question

The marginal cost of a product can be thought of as cost of producing one additional unit of output. For example, if the marginal cost of producing the 50th product is $6.20, it cost $6.20 to increase production from 49 units of output. Suppose the marginal cost C (in dollars) to produce X thousand MP3 players is given by the function c(x)=x^2-100x+7400.A.) how many players should be produced to minimize the marginal cost?B.) what is the minimum marginal cost?

Answer 1

a)

In order to find the number of players that should be produced to minimize the marginal cost, we just need to calculate the x-coordinate of the quadratic equation vertex.

This vertex represents the minimum point of the function (the point with the smallest value of y).

So, to find the vertex x-coordinate, we can use the following formula, after comparing the function with the standard form:

`\begin{gathered} f(x)=ax^2+bx+c \\ c(x)=x^2-100x+7400 \\ a=1,b=-100,c=7400 \\ \\ x_v=(-b)/(2a)=(-\mleft(-100\mright))/(2)=(100)/(2)=50 \end{gathered}`

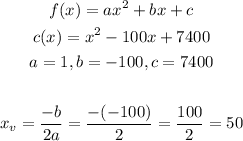
Therefore 50 players should be produced to minimize the marginal cost.

b)

To calculate the minimum marginal cost, let's use the number of players found in item a in the equation for the marginal cost:

`\begin{gathered} c(x)=x^2-100x+7400 \\ c(50)=50^2-100\cdot50+7400 \\ c(50)=2500-5000+7400 \\ c(50)=4900 \end{gathered}`

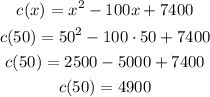
Therefore the minimum marginal cost is $4,900.