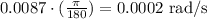Question

How fast is the angle of depression of the telescope changing when the boat is 260 meters from shore

Answer 1

Given:

The boat moves at a rate = 15 meters per second

The telescope is 40 meters above the water level

Let the distance between the boat and tower of the telescope = x

so,

`\begin{gathered} \tan \theta=(x)/(40) \\ \\ x=40\tan \theta \end{gathered}`

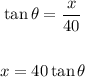
Differentiate both sides with respect to the time (t)

`(dx)/(dt)=40\cdot\sec ^2\theta\cdot(d\theta)/(dt)`

Where: (dx/dt) is the speed of the boat

(dθ/dt) is the change of the angle of the telescope

Substitute with (dx/dt = 15) and

When the boat is 260 meters from shore

`\begin{gathered} \tan \theta=(260)/(40)=6.5 \\ \theta=\tan ^(-1)6.5\approx81.254\degree \end{gathered}`

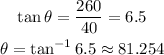
so,

`\begin{gathered} 15=40\cdot(\sec 81.254)^2\cdot(d\theta)/(dt) \\ \\ (d\theta)/(dt)=(15)/(40\cdot(\sec 81.254)^2) \end{gathered}`

Using the calculator:

`(d\theta)/(dt)=0.0087`

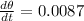
so, the answer will be 0.0087 degrees per seconds

Convert from to radians per second

So,

`0.0087\cdot((\pi)/(180))=0.0002\text{ rad/s}`