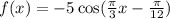Answer:
Given that:
The graph of a cosine function shows a reflection over the x-axis, an amplitude of 5, a period of 6, and a phase shift of 0.25 to the right.
To find the equation of the function described.
Step-by-step explanation:
we have that,
General formula of cosine function is,
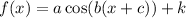
where a is amplitude, b is period factor, c is shift (left/right) and k is shift (up/down)
From given,
a=5
b=2pi/6=pi/3
c=0.25
we get,
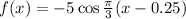
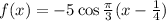
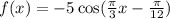
Answer is: option:b