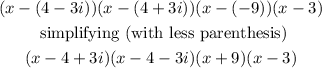Question

Given that 4 - 3i is a zero, factor the following polynomial function completely. Use the Conjugate Roots Theorem, if applicable. f(x) = r4 - 2x3 - 50x2 + 366x - 675

Answer 1

The factored polynomial is (x - 4 + 3i)(x - 4 - 3i)(x + 9)(x - 3)

Step-by-step explanation

The conjugate roots theorem tells us that if a+bi is a zero for the polynomial, then its conjugate a - bi is a zero too.

In this problem, it is given that 4 - 3i is a zero, then 4 + 3i is a zero too.

Therefore, the given polynimal can be divided by:

`\begin{gathered} (x-4+3i)(x-4-3i)=((x-4)+3i)((x-4)-3i) \\ \text{ by the difference of two squares rule:} \\ (x-4)^2-(3i)^2=(x^2-8x+16)-(-9)=x^2-8x+25 \end{gathered}`

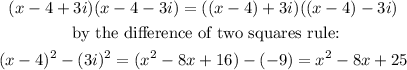
The division gives as a result this polynomial:

`x^2+6x-27`

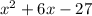
Which is a second degree polynomial and we can use this rule to find its two roots:

`\begin{gathered} ax^2+bx+c \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this polynomial a = 1, b = 6 and c = -27:

`\begin{gathered} x=\frac{-6\pm\sqrt[]{6^2-4\cdot1(-27)}}{2\cdot1} \\ x=\frac{-6\pm\sqrt[]{36+108}}{2} \\ x=\frac{-6\pm\sqrt[]{144}}{2}=(-6\pm12)/(2) \\ x_1=(-6-12)/(2)=(-18)/(2)=-9 \\ x_2=(-6+12)/(2)=(6)/(2)=3 \end{gathered}`

The other two roots (or zeros) of our polynomial are 3 and -9.

To write a factored polynomial, if x1, x2, x3 and x4 are roots, we have to write:

`(x-x_1)(x-x_2)(x-x_3)(x-x_4)`

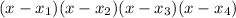
For our polynomial:

`\begin{gathered} (x-(4-3i))(x-(4+3i))(x-(-9))(x-3) \\ \text{ simplifying (with less parenthesis)} \\ (x-4+3i)(x-4-3i)(x+9)(x-3) \end{gathered}`