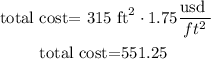Question

The measurements of a rectangular room, in a scale drawing, are 2 1/2 inches by 3 1/2 inches. The scale is 1/2 inch = 3 feet. If carpet costs $1.75 per square foot, how much will it cost to put carpet in this room?

Answer 1

$551.25

Step-by-step explanation

Step 1

convert the mixed numbers in fractions

`\begin{gathered} 2(1)/(2)=((2\cdot2)+1)/(2)=(5)/(2)=2.5 \\ 2(1)/(2)=2.5 \\ 3(1)/(2)=((3\cdot2)+1)/(2)=(7)/(2)=3.5 \\ (1)/(2)=0.5 \\ \\ \end{gathered}`

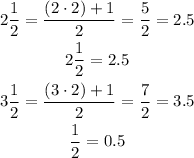
Step 2

find the factor of scale

remind 1 feet =12 inches

`\begin{gathered} 0.5\text{ inches in plane}\rightarrow3\text{ feet} \\ 0.5\text{ inches inplane}\rightarrow(3\cdot12) \\ 0.5\text{ inch plane}\rightarrow36\text{ inch in the reality} \\ \text{the ratio is} \\ 0.5\colon36 \\ 1\colon72 \end{gathered}`

it means, if you measure a inch in the drawing it corresponds to 72 inches in the real the room

Step 3

find the real measures

`\begin{gathered} (2.5)/(x)=(1)/(72) \\ 2.5\cdot72=x\cdot1 \\ x=180\text{ inches} \\ \text{divide by 12 to obtain feet} \\ 180\text{ inches}\rightarrow180\text{ inches}\frac{1}{12\text{ inches}}\rightarrow15\text{ feet} \\ so,\text{ a measure is 15 feet} \end{gathered}`

Step 4

`\begin{gathered} (3.5)/(y)=(1)/(72) \\ 3.5\cdot72=y\cdot1 \\ y=252\text{ inches} \\ \text{divide by 12 to obtain feet} \\ 252\text{ inches}\rightarrow252\text{ in}\frac{1\text{ feet}}{12\text{ inch}}\rightarrow21\text{ feet} \end{gathered}`

Step 5

find the area of the room

`\begin{gathered} \text{Area}=\text{ x}\cdot y \\ \text{Area}=\text{ 15 feet }\cdot\text{ 21 feet} \\ \text{Area = 315 ft}^2 \end{gathered}`

Step 6

finally, to obtain the total cost of the carpet, multiply the number of square feet by the cost per square foot of the carpet

`\begin{gathered} \text{total cost= 315 ft}^2\cdot1.75\frac{\text{usd }}{ft^2} \\ \text{total cost=551.25 } \end{gathered}`