Given,
The length of each side of the square, l=90 ft
In the diagram, h represents the home plate, 1 is 1st base plate, 2 is 2nd base, 3 is the third base.
The displacement can be defined as the shortest distance between two points.
1st base
The distance from the home plate to 1st base is,
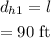
Thus the distance from home plate to 1st base is 90 ft
The shortest distance between the home plate and the 1st base is equal to the length of the side.
The displacement, in this case, is equal to the distance.
Thus the displacement of the player when he is at the 1st base plate is,
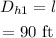
Thus the displacement of the player from home plate to 1st base is 90 ft
2nd base
The distance between the home plate and the second base is,
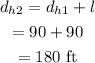
The distance covered by the player when he is at the second base is 180ft.
The displacement of the player from the home plate to 2nd base is given by the Pythagorean theorem.
That is,
![\begin{gathered} D_(h2)=\sqrt[]{d^2_(h1)+l^2_{}}=\sqrt[]{l^2+l^2} \\ =\sqrt[]{90^2+90^2} \\ =127.28\text{ ft} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/pqwd6semlxstzd8k1h7e.png)
Therefore, the displacement of the player as he reaches the second base is 127.28 ft.
3rd base
The distance covered by the player from the home plate to third base is,
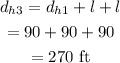
Thus the distance covered by the player from home plate to the 3rd base is 270 ft.
The displacement, i.e., the shortest distance from the home plate to the third base is,
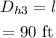
Thus the displacement of the player when he reaches the third base is 90 ft.
The home plate:
The distance covered by the player when he comes back to the home plate is,
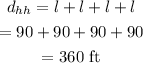
Thus, the distance covered by the player when he scores the home run is 360 ft.
The displacement of the player when he reaches the home plate is zero. As the shortest distance from home plate to home plate is 0 ft.