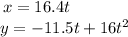Question

Rick shoots a basketball at an angle of 35' from the horizontal. It leaves his hands 7 feet from the ground with a velocity of 20 ft/s.Step 1 of 2: Construct a set of parametric equations describing the shot. Round all final values to the nearest tenth.Answer

Answer 1

Given:

The angle of projection of the basketball, θ=35°

The height at which the ball leaves the hand, h=7 ft

The initial velocity of the basketball, v=20 ft/s

To find:

The parametric equations describing the shot.

Step-by-step explanation:

The range, x of the basketball is given by,

`x=v\cos\theta t`

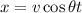
On substituting the known values,

`\begin{gathered} x=20*\cos35\degree* t \\ \implies x=16.4t \end{gathered}`

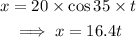
The change in the height, y of the basketball is given by,

`y=-v\sin\theta t+(1)/(2)gt^2`

Where g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} y=-20*\sin35\degree* t+(1)/(2)*32* t^2 \\ \implies y=-11.5t+16t^2 \end{gathered}`

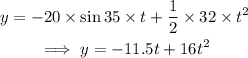
Final answer:

The parametric equations describing the shot are

`\begin{gathered} \begin{equation*} x=16.4t \end{equation*} \\ \begin{equation*} y=-11.5t+16t^2 \end{equation*} \end{gathered}`