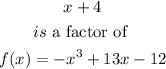Solution:
The first polynomial is given below as
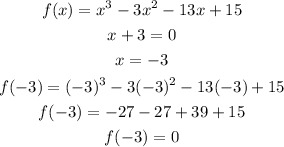
Hence,
The first answer is
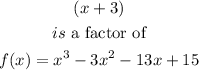
Step 2:
The second function is given below as
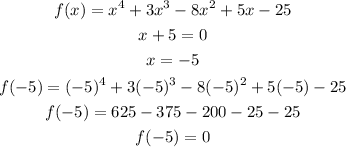
Hence,
The final answer is
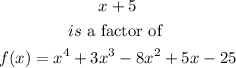
Step 3:
The fourth function is given below as
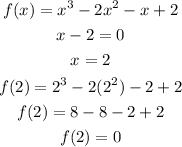
Hence,
The final answer is
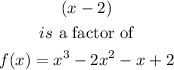
Step 4:
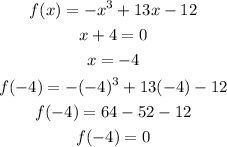
Hence,
The final answer is