Let's go over each line one by one and try to write an equation for them in the slope intercept form.
We can see line a is a vertical line. As such, we won't be able to write it in the form y=mx+b, but we can write it in the form x=my+b. Since it is parallel to the y-axis, the slope will be 0, and since it goes through the x-axis at x= -4, its equation will be
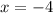
Similarly, we can see that line b is parallel to line a, so following the same resoning we'll get that its equation is
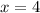
Line c is parallel to the x-axis, and it crosses the y-axis at y=4. Therefore, its equation is
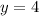
Likewise, line d is parallel to the x-axis, but it goes through the y-axis at y= -2, so its equation is
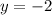
Finally, since line e isn't parallel to any of the axes, we'll need to determine two points it goes through in order to get its equation. We can see it goes through the intersection of lines a and c, and through the intersection of lines b and d.
In other words, it goes through the points (-4,4) and (4,-2).
Knowing this, we can calculate its slope using the formula
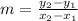
so in our case
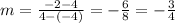
Usually we would use this slope and a known point to determine its y-intercept, but in this case we can s ee