Question

Solve the inequality and graph the solution set.|5-x|>6

Answer 1

From the problem, we have :

`\lvert5-x\rvert>6`

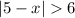
In solving absolute values, we need to take the positive and negative values of the terms outside the absolute value sign.

This will be :

`\begin{gathered} 5-x>6 \\ 5-x>-6 \end{gathered}`

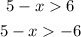
We will form two inequalities.

Solve for the solutions :

For the first inequality,

`\begin{gathered} 5-x>6 \\ -x>6-5 \\ -x>1 \\ \text{Note that multiplying a negative number will change the symbol} \\ \text{Multiply by -1} \\ x<-1 \end{gathered}`

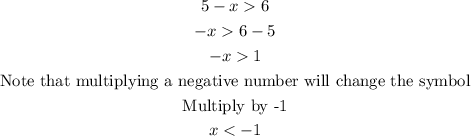
For the second inequality,

`\begin{gathered} 5-x>-6 \\ -x>-6-5 \\ -x>-11 \\ \text{Multiply by -1} \\ x<11 \end{gathered}`

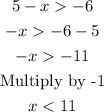
So we have x < -1 and x < 11

From these two solutions, x < -1 will govern since that inequality needs a value of x less than -1 and some of the numbers less than 11 will not apply to it.

So the answer is x < -1

The graph will be :

The end point is an open circle because the symbol is <