Question

A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 105.2-cm and a standard deviation of 1.7-cm. For shipment, 26 steel rods are bundled together.Find the probability that the average length of a randomly selected bundle of steel rods is less than 104.3-cm. P(M < 104.3-cm) =

Answer 1

We know the population distribution for the length of the rods: normal distribution with mean 105.2 cm and a standard deviation 1.7 cm.

In this case, we have a sample of 26 units, so we have to adjust the standard error to this sample size.

We have to calculate the probability that the sample mean is less than 104.3 cm.

We start by calculating the z-score for this sample mean value:

`\begin{gathered} z=(X-\mu)/((\sigma)/(√(n))) \\ \\ z=(104.3-105.2)/((1.7)/(√(26)))\approx(-0.9)/(0.3334)\approx-2.7 \end{gathered}`

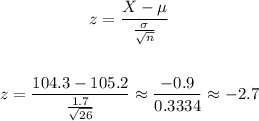
We can now calculate the probability by looking at the standard normal distribution:

`P(M<104.3)=P(z<-2.7)=0.00347`

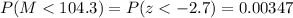
Answer: P(M < 104.3 cm) = 0.00347