Question

Explain:What is a periodic function? And what is the period? What is the amplitude? Label them on a graph(I may show you a graph and ask you to identify period and amplitude for example)

Answer 1

Define a periodic function:

A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals o radians, are periodic functions.

Take for instance a sine function below

Step 2:

Define the amplitude of a function:

The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine.

`\begin{gathered} From\text{ the sine function, the amplitude is represented as} \\ =A \end{gathered}`

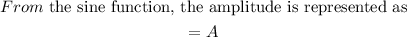
Step 3:

Define the period of a function:

The Period goes from one peak to the next (or from any point to the next matching point):

This is the time it takes complete one cycle

From the equation of a sine function,

The period is represented below as

`Period=(2\pi)/(B)`

TAKE FOR EXAMPLE ,

The sine equation given below

`\begin{gathered} y=2sin(4(x-0.5))+3 \\ Amplitude=A=2 \\ period=(2\pi)/(B)=4 \\ period=B=(\pi)/(2) \end{gathered}`

The graph will be given below as