We have a bag of marbles with an unknown amount inside. We only now that if we split the number between 4,6 or 18 people, there are none left. This means, mathematically, that the quantity inside is a multiple of 4, 6 and 18. Since we want to calculate the smallest number of marbles that could be inside, this means that we want to calculate the least common multiple of 4, 6 and 18.
To do this, we proceed as follows.
First, we write all three numbers one next to the other.
4 6 18
Now, we will search among the prime numbers, which one divides at least one of them. We keep doing so until we have divided all numbers so we get the number 1 Recall that the list of the first 10 prime numbers is 1,2,3,5,7,11,13,17,19,23.
So, at the beginning 4, 6 and 18 can be all divided by 2 (we keep this number in mind), then we choose 2. If we divide each number by 2, we get
2 3 9
Now, we repeat the process. Since 3 and 9 are multiple of 3, we choose 3. So now we divide 3 and 9 by 3, so we get
2 1 3
Now, we can divide 2 by 2, so we get
1 1 3
Finally, we divide 3 by 3, so we get
1 1 1
So, the numbers we chose the numbers 2,2,3,3. We multiply them all together and we get
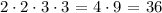
So the smalles number of marbles that could be in the bag is 36.