Question

Identify the absolute extrema of the function642f(x) = 2x +X+1, x>0

Answer 1

We are given the following function and we have to find its absolute minimum:

`f(x)=2x+64x^(-2)+1,x>0`

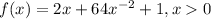
The first step to solve this problem would be to take the derivative of the function and set it equal to 0. This is because extrema occur at points where the slope is equal to 0:

`f^(\prime)(x)=2+(-2)64x^(-3)=2-128x^(-3)`

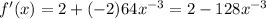
Now, let's set the function to 0 and solve for x:

`\begin{gathered} 2-(128)/(x^3)=0 \\ 2=(128)/(x^3) \\ 2x^3=128 \\ x^3=64 \\ x=4 \end{gathered}`

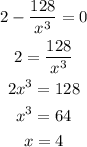
Now we know that there is one critical point, which occurs when x equals 4. Since there is only one critical point, this must be the absolute minimum value. We can now plug x=4 into the original function to solve for the y value:

`\begin{gathered} f(x)=2x+(64)/(x^2)+1 \\ f(4)=2(4)+(64)/(4^2)+1=8+(64)/(16)+1=8+4+1=13 \end{gathered}`

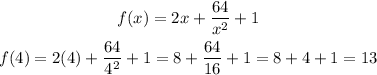
Therefore, the absolute minimum is 13 and occurs at the x-value 4 (minimum corresponds to the y-value that we calculated)